Abstract
The elusive supermassive black hole binaries (SMBHBs) are thought to be the penultimate stage of galaxy mergers, preceding a final coalescence phase. SMBHBs are sources of continuous gravitational waves, possibly detectable by pulsar timing arrays; the identification of candidates could help in performing targeted gravitational wave searches. Due to SMBHBs' origin in the innermost parts of active galactic nuclei (AGN), X-rays are a promising tool for unveiling their presence, by means of either double Fe Kα emission lines or periodicity in their light curve. Here we report on a new method for selecting SMBHBs by means of the presence of a periodic signal in their Swift Burst Alert Telescope (BAT) 105 month light curves. Our technique is based on Fisher's exact g-test and takes into account the possible presence of colored noise. Among the 553 AGN selected for our investigation, only the Seyfert 1.5 galaxy Mrk 915 emerges as a candidate SMBHB; from subsequent analysis of its light curve we find a period P0 = 35 ± 2 months, and the null hypothesis is rejected at the 3.7σ confidence level. We also present a detailed analysis of the BAT light curve of the only previously X-ray-selected binary candidate source in the literature, the Seyfert 2 galaxy MCG+11-11-032. We find P0 = 26.3 ± 0.6 months, consistent with the one inferred from previously reported double Fe Kα emission lines.
1. Introduction
It is now well established that massive galaxies host supermassive black holes (SMBHs, MBH ≳ 106 M⊙) in their central regions (e.g., Kormendy & Ho 2013). Such extreme astrophysical objects are likely linked to the evolution of their host galaxies. In fact, stellar bulge properties, such as velocity dispersion (e.g., Ferrarese & Merritt 2000) and stellar mass (e.g., Häring & Rix 2004), are found to correlate with the mass of the central SMBH.
In Λ cold dark matter (ΛCDM) cosmological models galaxies grow hierarchically through frequent mergers (e.g., Cole et al. 2000; Volonteri et al. 2003). Galaxy mergers have been proposed as one of the main mechanisms by which nuclear activity, star formation and outflows are triggered (e.g., Di Matteo et al. 2005; Hopkins et al. 2006; Di Matteo et al. 2008). One of the most interesting possible outcomes of this process is the formation of an SMBH binary (SMBHB) system. During a galaxy merger, if both SMBHs are accreting at kiloparsec-scale distance from each other, the source will appear as a dual active galactic nucleus (AGN; e.g., Koss et al. 2012; McGurk et al. 2015; De Rosa et al. 2018, 2019; Koss et al. 2018, and references therein). Subsequently, the two SMBHs drift toward the center of mass because of dynamical friction (Dosopoulou & Antonini 2017) and form an inspiraling binary system at subparsec-scale separations (e.g., Begelman et al. 1980), which will eventually merge (e.g., Dotti et al. 2012; Mayer 2013; Colpi 2014). Theoretical models predict that, after the two black holes bind in a binary, dynamical friction becomes inefficient, possibly preventing the binary from merging in a time shorter than the Hubble time (e.g., Milosavljević & Merritt 2003). However, in the presence of nuclear gas inflows (e.g., Dotti et al. 2012), or deviations from spherical symmetry in the potential of the nucleus (Sesana & Khan 2015), the binary can still transfer enough energy to its surroundings to merge within tcoal ∼ 1 Gyr. Despite the expected abundance of such objects, the detection of SMBHBs remains elusive and only limited indirect observational evidence has been found so far (see De Rosa et al. 2019 for a recent review). This is mainly due to the angular resolution of current telescopes, which do not have a resolving power below a few parsecs at most redshifts and wavelengths (e.g., Rodriguez et al. 2006), insufficient to distinguish emitting binary systems.
Hydrodynamic numerical simulations usually assume that an SMBHB excavates a cavity in the surrounding gas, which forms a circumbinary accretion disk (e.g., Noble et al. 2012; Farris et al. 2015). At smaller scales, accretion possibly occurs through minidisks around each black hole inside the cavity (e.g., Hayasaki et al. 2008; D'Ascoli et al. 2018). While the circumbinary disk is thought to be responsible for the optical and IR emission (D'Orazio et al. 2015), the UV and X-rays should be mainly emitted by the inner minidisks (Sesana et al. 2012; D'Ascoli et al. 2018). In particular, the UV and X-ray fluxes are expected to be periodic, since the accretion rate of the minidisks is periodically fed by streams of gas flowing from the outer circumbinary disk (e.g., Hayasaki et al. 2008; Haiman et al. 2009; Farris et al. 2015), with periods comparable to the binary period. Assuming a Keplerian regime, for SMBHBs with a separation of the order of 10−3 pc, we expect a periodicity with periods longer than about a year. As these emissions originate very close to each black hole, UV and X-ray periodic modulation (e.g., Sesana et al. 2012; Roedig et al. 2014; Farris et al. 2015; Haiman 2017) can be used to identify possible SMBHBs. Additionally, the two minidisks may produce double-peaked Fe Kα emission lines in the X-ray band (e.g., Popović 2012; Sesana et al. 2012; McKernan & Ford 2015), with energies Doppler-shifted by the minidisk relative to orbital motion. So far, the only X-ray-selected SMBHB candidate is the Seyfert 2 galaxy MCG+11-11-032 (Severgnini et al. 2018). The detection of two peaks (at 4σ and 2σ, respectively) in the Fe Kα energy range, along with the visually identified harmonic behavior of the 123 month Swift Burst Alert Telescope (BAT) X-ray light curve with a period of P ∼ 25 months, strongly suggests the presence of an SMBHB.
Periodical variability from the inflow streams is also expected in the optical band, although it may be overwhelmed by the non-periodic emission from the circumbinary disk. Despite the fact that the UV and X-ray data are likely the best electromagnetic (EM) bands for periodicity searches in AGN, regular monitoring observations in these bands, spanning several years, are rare. For these reasons, the search for EM periodicity has been mainly undertaken in the optical band. Graham et al. (2015a) found 111 optically selected SMBHB candidates in the Catalina Real-Time Survey (Drake et al. 2009), and Charisi et al. (2016) identified 33 further objects in the Palomar Transient Factory (Rau et al. 2009). In addition, the presence of a periodic signal has been reported in single-source studies, such as of OJ 287 (e.g., Sillanpaa et al. 1988), PG 1302-102 (Graham et al. 2015b), NGC 5548 (Bon et al. 2016; Li et al. 2016), and more recently Mrk 231 (Kovačević et al. 2020). In particular, OJ 287 shows recurring flares with a precision so high that it is possible to predict the following flare with an accuracy of ∼4 hr on a ∼12 yr period (Laine et al. 2020). However, a significant fraction of those candidates are likely false positives. In fact, such a large number of SMBHBs should have produced a gravitational wave (GW) cosmic background above the current pulsar timing array (PTA) limit (see Arzoumanian et al. 2018 for the latest NANOGrav Collaboration limit, Lentati et al. 2015 for the latest European PTA limit, and Shannon et al. 2015 for the Parkes PTA limit), while no detection has been reported so far (Sesana et al. 2018).
By exploiting the 105 Month Swift-BAT Survey (Oh et al. 2018), here we propose a novel method to search for periodicities in colored noise X-ray light curves based on Fisher's exact g-test (Fisher 1929) and its probability of false alarm due to colored noise fluctuations. A recent analysis of the X-ray light curves of a subsample of ∼220 AGN, selected by their large excess variance,16 of the BAT survey (Liu et al. 2020) did not find any AGN with evidence for periodic behavior in their X-ray light curves. The search was based on the power spectrum fitting (Vaughan 2005) of colored noise light curves, i.e., those curves whose power spectral densities are not flat, or white (see Section 3 for details).
The paper is structured as follows: in Section 2 we review the power spectrum and the X-ray variability tools usually adopted, while in Section 3 we describe the proposed search method on simulated light curves. In Section 4 we apply the method to real X-ray light curves in the 105 Month Swift-BAT Survey and test the selected candidates by using sinusoidal fitting and epoch folding techniques. MCG+11-11-032 is also discussed in Section 5. Finally, we summarize and discuss our results in Section 6.
Throughout the paper, we adopt a flat ΛCDM cosmology H0 = 70 km s−1 Mpc−1, ΩΛ = 0.7 and ΩM = 0.3.
2. Identifying a Periodic Trend in a Stochastic Light Curve
X-ray emission from AGN is well known to be very variable (e.g., Markowitz & Edelson 2004; McHardy et al. 2004; Vagnetti et al. 2016; Falocco et al. 2017), even at hard energies (E > 10 keV; e.g., Soldi et al. 2014). The X-ray variability of AGN is typically a superposition of stochastic processes and therefore is not easily modeled as a function of time and is usually referred to as noise.
Identifying periodic trends in light curves may result in a challenging task, because a sinusoidal or quasi-sinusoidal curve may be hidden in noise and be hardly recognizable in the time domain. A very powerful tool for identifying periodicities is the power spectral density (PSD), or power spectrum, which represents the mean value of the squared amplitude as a function of the temporal frequency f. The most frequently used tool to represent the power spectrum is the periodogram PS(f), which is defined as the squared Fourier transform of the light curve, i.e., , where is the Fourier transform of the light curve x(t) and its complex conjugate.17 We subtract the mean value of the light curve before computing the Fourier transform, to remove the constant component of the light curve. We also neglect all frequency values larger than or equal to the Nyquist frequency fNyq = 1/2δt, where δt is the sampling time, and their corresponding periodogram values, in order to exclude points due to aliasing. Several normalizations may be defined for the periodogram (e.g., Papadakis & Lawrence 1993; Vaughan et al. 2003; Emmanoulopoulos et al. 2016), but since we intend to study individual sources one by one (see Section 4), we choose a unitary normalization, and therefore . This quantity is ideal for finding periodicities, given that the response to a pure sinusoid is a Dirac δ-function. PSD is regularly used to identify periodicities in pulsar astronomy at many EM bands (e.g., Israel et al. 2016; Ambrosino et al. 2017; Mickaliger et al. 2018), to search for their continuous GW counterparts (e.g., Aasi et al. 2015), to detect quasi-periodic oscillations in X-ray binaries (e.g., Zhang et al. 1996), and to search for both short-term (e.g., Gierliński et al. 2008; Miniutti et al. 2019) and long-term periodicities in AGN light curves (e.g., Bon et al. 2016; Liu et al. 2020). Moreover, the Fourier transform operator is linear, and if our light curve is given by the superposition of a sinusoidal signal and random noise, i.e., , the resulting Fourier transform will be the sum of the transforms of the two components, i.e., , where for a sinusoidal component with temporal frequency f0. If the light curve is sufficiently long, an analysis in the frequency domain will identify the periodicity, even if a sinusoidal signal with a small amplitude does not manifest in the light curve due to a low signal-to-noise ratio. This is evident in Figure 1, where we simulate a white noise–dominated time series, superposed to a signal with amplitude 10 times smaller than that of the noise. While inspection of the time series does not show any evidence for the presence of a periodicity, the power spectrum shows an evident peak at f0 = 10−3 Hz, corresponding to the simulated sinusoid frequency.
Figure 1. Left. Light curve of 100 ks simulated data, sampled at 1 s and produced by the superposition of stochastic white noise and a sinusoid whose amplitude is set to 0.1 times the standard deviation of the noise and whose period is set to P0 = 1 ks. No evident periodicity can be inferred. Right. The periodogram of the same light curve shown in the left panel, showing a significant δ-like peak at f = 10−3 Hz.
Download figure:
Standard image High-resolution image2.1. Computing Significance above Underlying White Noise
Depending on the power of the periodic component with respect to the underlying noise, the peak in the periodogram will be more or less prominent. Typically, the greater the number of periods sampled in the light curve, the more prominent the periodic peak in the frequency domain, but quantifying its significance is not trivial. A common tool for estimating the significance of a peak above the underlying white noise is so-called Fisher's exact g-test (Fisher 1929). If one wants to analyze a peak at the frequency f0, the test consists in computing the value
where N is the number of points in our periodogram. The value g0 corresponds to a p-value of
where , i.e., the largest integer smaller than 1/g0. Given the presence of factorial calculations, Equation (1) is computationally impractical for very long light curves. We test whether our software is able to compute g-test p-values for light curves with up to ∼5 × 103 data points. Computing p-values of longer time series hence requires other tests to be used, but it is beyond the scope of this paper.
3. Simulations of Colored Noise Light Curves
The validity of the g-test is unfortunately limited to cases in which non-periodic noise is white. In fact, the power spectrum of the stochastic component of an AGN X-ray light curve is typically modeled as , in the absence of slope breaks in the sampled frequency range. In the case of white noise PSD, the slope α will be approximately zero. However, it is well known that underlying noise in X-ray light curves of AGN is not white; typically, one finds colored noise distributions, with slope values of α ∼ −1.5 in the frequency range (e.g., Green et al. 1993; Lawrence & Papadakis 1993; Allevato et al. 2013; Emmanoulopoulos et al. 2016). Ignoring the fact that the noise is colored can either lead to false positives (e.g., Vaughan et al. 2016), because the peak is tested against a flat noise instead of an fα noise, or hide true positives, which may be below overwhelmingly large noise fluctuations at low frequency. In such cases the result of the g-test cannot be used as is and we need a way to take the underlying slope of the PSD into account.
In order to evaluate the validity of the g-test in a colored noise PSD, we run simulations to assess the false alarm rate caused by the colored noise. To date, the only X-ray survey that at least partially samples the temporal frequency of interest ( Hz, corresponding to orbital periods of P ∼ 9–400 months), matching the frequency range where PTAs are most sensitive (e.g., Lentati et al. 2015; Moore et al. 2015; Shannon et al. 2015; Mingarelli et al. 2017; Arzoumanian et al. 2018), is the 105 Month Swift-BAT Survey (Oh et al. 2018). The survey provides Crab-weighted light curves binned at 1 month for 1631 sources, detected at a >5σ confidence level (see Baumgartner et al. 2013 for details). It covers almost half the sky at the energy range E = 14–195 keV and is therefore unlikely to have been affected by neutral or ionized absorbers, soft excess or other spectral features not associated with the primary emission. An analysis of the real Swift-BAT data is presented in Section 4.
We base our simulations on mock light curves that have the same characteristics as the real data that we intend to analyze. We only consider the AGN in the catalog, whose average count rates are distributed as shown in Figure 2. We then select only the brightest half of the sample, rightward of the vertical red dashed line, which represents the median count rate value (see Section 4), counting a total of 553 AGN.
Figure 2. Distribution of mean 14–195 keV count rates of each Swift-BAT light curve of the whole 1103 AGN sample. The vertical red dashed line is the median value, corresponding to .
Download figure:
Standard image High-resolution imageWe simulate 105 month long light curves with Gaussian-distributed count rates, i.e., white noise light curves. The mean of the Gaussian distribution is a typical value in the considered count rate range, while the standard deviation is the mean value of the photometric error. We verify that the results do not depend on the particular mean value we adopt in the range −3.3 ≲ log (CR/cts s−1) ≲ −1.5, or on the average value of the photometric error.
For N sources with white noise light curves, the probability of finding one false periodicity by chance is given by , which is p = 0.0018 for N = 553. Therefore, the g-test significance for white noise power spectra will be considered acceptable if the p-value satisfies . To check this procedure, we simulate 106 purely white noise light curves, i.e., without any injected periodicity, we perform g-tests on each and we flag every source with pval ≤ pth. The false alarm probability is given by the number of flagged light curves over the total number. As expected, we find . This is clearly not true for ; therefore we need to simulate light curves for different values of α and thus calculate .
In order to simulate colored noise light curves, we adopt the technique presented by Kasdin (1995), which we summarize in the following. We simulate a white noise light curve as previously described, and its Fourier transform is . It is possible to simulate a colored noise light curve, described by its spectral slope α, by defining the filter . We can introduce the quantity , whose inverse Fourier transform is x(c)(t). The periodogram of such a light curve is ; therefore by construction the simulated light curve x(c)(t) is made up of a stochastic colored noise process with spectral slope α.
These simulations can be used to quantify the expected number of false alarms in colored noise curves. We consider α in [−2, 1], spaced by δα = 0.01. For each value of α we simulate 106 light curves following the above-described procedure. Again, for each value of α, we count the light curves with pval ≤ 0.0018 and divide such number by 106, hence tracing in the selected interval, as shown in Figure 3.
Figure 3. False alarm probability as a function of the power spectral slope α. For each value of α in the range [−2 1], with δα = 0.01, we simulate 106 light curves, without injecting a periodic signal. For a given α, the false alarm probability is the number of curves with peaks with p-values lower than the chosen one, i.e., pval ≤ pth = 0.0018.
Download figure:
Standard image High-resolution image4. Analysis of Real Swift-BAT Data
4.1. Identification of Periodic Candidates
A first step to identify candidates is to perform g-tests on the sample of 553 Swift-BAT sources presented above, using the following multi-step approach: (i) we do not make any assumption on the nature of the stochastic noise of the light curves, i.e., we assume that they are all characterized by white noise. (ii) We identify the highest PSD peak, and we test such a peak against the rest of the PSD, assumed as noise. We only consider peaks at periods 9 ≲ P0 ≲ 35 months. The lower limit is set by the PTA sensitivity curve (e.g., Lentati et al. 2015), while the upper limit is set by the requirement that we observe at least three phases in a 105 month light curve, i.e., 105/3 = 35 months. (iii) We select all those sources whose p-values satisfy the condition pval ≤ 1/553 = 0.0018, which is the threshold corresponding to the probability of finding one false positive by chance in the total sample analyzed, without setting any prior. (iv) Once the candidates are identified, we investigate whether they are dominated by colored noise fluctuations or not, and then estimate the probability that the periodic component is real.
Only two sources survive the first screening. The first one is the blazar Mrk 421, which has a PSD peak at f0 = 18 ± 2 nHz, corresponding to a period of P0 = 21 ± 2 months, with pval = 5 × 10−4. The other selected AGN is the Seyfert 1.5 galaxy Mrk 915, with a PSD peak at f0 = 11 ± 2 nHz, corresponding to the period months, with pval = 8 × 10−4, a factor of about 3.6 and 2.3 below the threshold pval = 0.0018, respectively. We note that the uncertainties are given by the frequency resolution of the PSD at the peak frequency f0.
The initial screening does not take into account the intrinsic color of the stochastic noise, i.e., the slope of the PSD. Assuming a simple power-law model with no breaks in the sampled frequency range for the PSD, i.e., PS(f)∝fα, the slope can be computed with linear fits between the logarithmic values of and (e.g., Papadakis & Lawrence 1993). We compute α for each source, with its normalized distribution shown in Figure 4. We note that the bulk of our sample has PSD slopes −0.5 ≲ α ≲ 0.5, with a tail of very few sources characterized by α ≲ −0.5. Even though the typical slope at higher frequencies is α ∼ −1.5 (e.g., Allevato et al. 2013), this result is not surprising, since the X-ray PSD of AGN is expected to break to lower slopes at frequencies f ≲ 10−6 Hz (Shimizu & Mushotzky 2013), with PSD breaks observed in a few sources so far (Markowitz et al. 2003; McHardy et al. 2007; MacLeod et al. 2010). For this sample, a break timescale smaller than the Nyquist period, i.e., Tbr ≲ 2 months (or fbr ≳ 2 × 10−7 Hz), for 98% of the sources has been estimated by Liu et al. (2020), which means that the PSD break happens at much shorter timescales than those sampled by Swift-BAT, explaining the distribution of α shown in Figure 4.
Figure 4. Distribution of the PSD slope α for the 553 AGN sources considered in this work. The distribution is normalized to unity in order to represent the probability distribution function of finding a light curve with slope α.
Download figure:
Standard image High-resolution imageThe slopes of the PSDs for the two g-test selected candidates, Mrk 421 and Mrk 915, are α = −1.2 ± 0.2 and α = −0.4 ± 0.3, respectively. This means that Mrk 421 is one of those outliers that maintain red noise behavior even at extremely low frequencies, while Mrk 915 is characterized almost completely by white noise. We estimate the number of expected false alarms as the product of the false alarm probability for a given α, (see Figure 3), and the probability of α, p(α) (see Figure 4), multiplied by the number of sources N = 553, i.e., . Concerning Mrk 915, for α = −0.4 we re-simulate , using as the threshold, obtaining expected false alarms. As for Mrk 421 (α = −1.2, ), we obtain . This means that, assuming Poissonian distributions with expected value Nexp, the probability that Mrk 915 is a false positive is ∼6%, while for Mrk 421 such probability is ∼32%.
The high chance of Mrk 421 being a non-periodic component is supported by the fact that the source is well known to recurringly flare in all bands (e.g., Aleksić et al. 2015), including the X-ray bands (e.g., Stroh & Falcone 2013; Hervet et al. 2019). As shown in Figure 5, the source has numerous flares of various intensities at ∼20, ∼41, ∼63 and ∼83 months from the beginning of the survey. It is therefore straightforward to conclude that the PSD indeed indicates a recurring variability pattern with a typical timescale of P0 ∼ 21 months, but it is clearly not due to a proper sinusoidal behavior of the light curve. Moreover, it is well known that, for blazars like Mrk 421, the dominant X-ray emission mechanism is related to the presence of a jet rather than accretion (e.g., Fossati et al. 1998; Ghisellini et al. 2017).
Figure 5. Hard X-ray light curve of Mrk 421. The errors are omitted, since they are extremely small. Points are connected to highlight the flaring nature of the light-curve variability. The arrows indicate four possible flares, happening at ∼21 months from each other, with different intensities.
Download figure:
Standard image High-resolution imageWe conclude that Mrk 421 is not a binary candidate, according to our selection criteria, while Mrk 915 deserves a closer look at its light curve.
4.2. Light-Curve Analysis of Mrk 915
As reported in the previous section, the variability pattern of Mrk 915 possibly includes a periodic component with frequency f0 = 11 ± 2 nHz, corresponding to a period of months (see Figure 6). However, the g-test does not allow us to assess an absolute statistical significance, since it is tested near the boundary condition (see Protassov et al. 2002 for details), so it is only used to screen potential interesting candidates in our work. Moreover, the g-test does not take the photometric errors into account and, therefore, if the errors are large, i.e., their excess variance is small or negative, the periodicity might be apparent and must be tested with other methods. In the specific case of Mrk 915, the excess variance is negative, which implies that the observed variability could be apparent, and hence the PSD analysis must be handled with care and the putative periodicity should be investigated further.
Figure 6. PSD of Mrk 915. The red vertical dashed line represents the peak at f0 = 11 ± 2 nHz (or months).
Download figure:
Standard image High-resolution imageIn order to investigate this and to take the errors into account we first attempt a simple weighted least-squares sinusoidal fit of the light curve.18 The fitted function is given by , where A0, A1, t0, and P0 are all free parameters. We obtain the following best-fit values, with errors given at a 90% confidence level:
The goodness of fit is given by . In Figure 7 we show the Swift-BAT light curve, overlapped by its best-fit sinusoidal curve. We note that the best-fit value of P0 is consistent with the corresponding value of the PSD peak that is found with the g-test sample screening.
Figure 7. Hard X-ray light curve of Mrk 915. The red line represents the best-fit sinusoidal curve.
Download figure:
Standard image High-resolution imageWe use this latter result to perform a phase folding procedure on the light curve of Mrk 915 (e.g., Leahy et al. 1983). The epoch folding search is typically used to determine the period and the amplitude of the sinusoidal trend (see, e.g., Leahy 1987). However, given the short effective exposure time and the large period (P0 ≃ 35 months), it is not possible to oversample the Fourier resolution (). Therefore, we use P0 as a known parameter to fold the data set with n = 6 phase bins and test the null hypothesis. The number of bins is chosen as a trade-off between a high signal-to-noise ratio for each bin and the fact that significance tests, such as the χ2 test, are more reliable with more data points available.
We first compute the relative phase of each monthly observation as
where t is the time relative to the points of the light curve shown in Figure 7, and is the integer part of a. We then combine the count rates corresponding to all points belonging to the same phase bin with the relative 1σ uncertainty. Given a set of N observations with count rate and exposure δti, the count rates are combined as their weighted mean
while the errors are given by
This procedure is repeated for all the six phase bins we divide the period into. The folded light curve is shown in Figure 8.
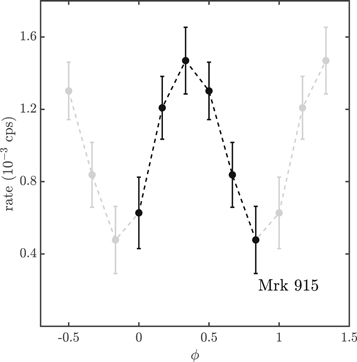
Figure 8. Phase folding of the Mrk 915 hard X-ray light curve. The folding period is divided into six phase bins, each combining ∼16 light-curve data points. The gray points are mirrored from the six main phase bins, in order to highlight the periodical trend.
Download figure:
Standard image High-resolution imageTo confirm the presence of a periodic trend, we test the null hypothesis with a χ2 test on the folded light curve, obtaining χ2 ≃ 24, corresponding to a p-value of 2.3 × 10−4 for 5 degrees of freedom (i.e., six phase bins minus one), which means that we are able to reject the null hypothesis with a confidence level of 3.7σ.
5. Light-Curve Analysis of MCG+11-11-032
As shown in Section 4, our method only selects one SMBHB candidate from the AGN sample. It must be stressed, though, that the method is very conservative, and aims at selecting only the strongest candidates. Indeed, the only previously X-ray-selected SMBHB candidate (Severgnini et al. 2018), the Seyfert 2 galaxy MCG+11-11-032, is included in our Swift-BAT sample, but is excluded with the g-test selection criteria. It must be noted that the p-value threshold is low because we do not consider in this work periodicities with significance below . This does not mean that a periodic trend, which may be hidden by the noise, or hidden by large measurement errors, is not present. As shown in Figure 9, the highest value of the PSD is found at f0 = 15 ± 2 nHz, which corresponds to months, with pval > 0.0018, i.e., not significant. The PSD slope is given by α = 0.4 ± 0.3 and is therefore consistent with white noise at a 90% confidence level. However, this Seyfert 2 galaxy was identified as a possible SMBHB candidate by means of the presence of two Fe Kα emission lines at energies E = 6.16 ± 0.08 keV and E = 6.56 ± 0.15 keV, at 4σ and 2σ confidence levels, respectively. Such lines, if emitted by two separate sources in the center of the AGN, would imply that they are red- and blueshifted Fe Kα emission lines by two minidisks, orbiting each other with a period of P0 ∼ 25 months.
Figure 9. PSD of MCG+11-11-032. The red vertical dashed line represents the peak at nHz (or months).
Download figure:
Standard image High-resolution imageThe possible presence of a double Fe Kα emission line justifies an exception on the PSD screening and further investigation of this source. Therefore, we analyze the light curve of MCG+11-11-032, using the same procedure as that used for Mrk 915. We perform a weighted sinusoidal fit, testing again the function . The best-fit values, with errors given at a 90% confidence level, are
with a goodness of fit of . The period derived is in agreement with the estimate given by Severgnini et al. (2018). Furthermore, in this case the period found with the sinusoidal fit is similar to the period corresponding to the maximum value of the PSD (Figure 9).
To further investigate MCG+11-11-032, we use the procedure adopted in Section 4.2 to perform epoch folding of the light curve of MCG+11-11-032, adopting six phase bins (red points in Figure 10). Also in this case we test the null hypothesis using a χ2 test, obtaining χ2 ≃ 15, which corresponds to a p-value of pval = 0.0097 for 5 degrees of freedom. This means that the null hypothesis is rejected at the 2.6σ confidence level.
Figure 10. Phase folding of the MCG+11-11-032 hard X-ray light curve. The folding period is divided into six phase bins. The gray points are copies of the six main bins, in order to highlight the periodic behavior. The red points are the result of the epoch folding of the 105 Month Swift-BAT survey light curve, while the black points represent the folding of the Swift-BAT 123 month long light curve, in the E = 15–150 keV energy band. The two curves have different count rates, because of different normalizations (see Segreto et al. 2010; Baumgartner et al. 2013, for further details).
Download figure:
Standard image High-resolution imageAssuming that the double Fe Kα spectral feature and the sinusoidal trend are the result of two different experiments of the same physical scenario, i.e., the presence of an SMBHB system, we use the meta-analysis technique called Fisher's combined probability test (Mosteller & Fisher 1948). Given k independent experiments, each resulting in its own p-value , the test consists in computing the following statistic:
where is distributed as a with 2k degrees of freedom, and can be therefore tested as such. Since in our case k = 2, we test against a χ2 distribution with 4 degrees of freedom. In Severgnini et al. (2018) a significance of 2σ (pval = 0.05) was reported for the least significant emission line. Using Equation (2) to combine such a p-value with the one obtained with the epoch folding we obtain , corresponding to a global combined p-value of pval = 0.0042 for 4 degrees of freedom. This means that, under the assumption that the spectral emission lines and the periodicity are both caused by the presence of a binary system, we are able to reject the null hypothesis of non-binarity with a 2.9σ confidence level.
As shown in Figure 10, the M-shape of the epoch folding plot suggests the possible presence of two harmonics. We add a second harmonic component to the fitting model, i.e., we fit the function sin + . We find a goodness of fit of , with an improvement given by , meaning that the addition of the second harmonic is not significantly required by the data. However, we note that the best-fit period, P0 = 25.9 ± 1.5 months, is consistent with the one found by fitting only one sinusoidal component. A longer light curve, possibly with a lower noise level, would be required to confirm the presence of a possible second harmonic component.
For this source, we also consider the 123 month 15–150 keV Palermo Swift-BAT light curve (Segreto et al. 2010), available only for this AGN, which was already presented in Severgnini et al. (2018) (Palermo Swift-BAT team, private communication). Assuming the derived period of ∼26 months, this longer light curve samples almost five periods and could in principle return a higher significance for rejecting the null hypothesis. We bin the light curve at 5 months of observations per data point, to maximize the signal-to-noise ratio. The curve is well fitted by a single sinusoid , with a goodness of fit of , and a best-fit period P0 = 26.0 ± 0.6 months, consistent with the best fit obtained with the 105 month light curve. We use such a period to undertake the epoch folding technique, shown in Figure 10 (black points). We test the null hypothesis with a χ2 test, obtaining χ2 ≃ 21, which corresponds to pval = 7.5 × 10−4, implying that for this longer light curve the null hypothesis can be rejected at the 3.4σ confidence level. Considering also the result in Severgnini et al. (2018) in the combined probability test (Equation (2)), we obtain pval = 4.2 × 10−4, which means that the null hypothesis can be rejected with a 3.5σ confidence level. The black points in Figure 10 also suggest in this case the presence of a second harmonic. However, adding a second harmonic component in the light-curve fit still produces a consistent period (P0 = 26.1 ± 0.8 months), but the goodness of fit is ; hence the second harmonic is required by the F-test at only the 93% confidence level.
6. Discussion and Conclusions
We have presented a method for selecting SMBHB candidates using Fisher's exact g-test, finding a candidate in the Seyfert 1.5 galaxy Mrk 915 with a period given at the maximum value of the PSD of months. This source is not affected by colored noise, since the slope of its PSD is given by α = −0.4 ± 0.3, implying almost completely white noise, and there is only a 6% probability of the periodicity being a false positive. As a follow-up to this selection, we perform a sinusoidal fit on the Swift-BAT hard X-ray light curve spanning 105 months, and we find a period of P0 = 35 ± 2 months, consistent with the period corresponding to the maximum PSD value, with a goodness of fit of . Furthermore, we test such a period with an epoch folding procedure, finding that the null hypothesis can be rejected with a 3.7σ confidence level. Assuming a Keplerian orbit, the distance a between the two X-ray-emitting regions that embed the two SMBHs can be inferred by using Kepler's third law, i.e., , where M is the total mass of the two black holes, P0 is the measured period, and G is the gravitational constant. We adopt the black hole mass estimate , computed using single-epoch Hβ measurements (Bennert et al. 2006). We derive a distance between the two hard X-ray-emitting regions of a = (5 ± 1) × 10−3 pc. Assuming a circular orbit, the relative velocity between the putative black holes is . Previous X-ray spectroscopy analyses of the source (e.g., Severgnini et al. 2015; Ballo et al. 2017) have not unveiled any double Fe Kα feature. In particular, XMM-Newton, with its energy resolution of ∼0.15 keV at the line energy, detects a single Fe Kα line at E = 6.42 ± 0.02 keV with no double peaks (Ballo et al. 2017). We can therefore conclude that, if the binary system is able to produce a double peak, the energy separation between the two peaks would be ΔE ≲ 0.15 keV. Given the orbital velocity Δv obtained from the measured period, the expected Fe Kα energy shift is given by , where and ι is the inclination angle. Since XMM-Newton only observes one emission line, if two peaks are indeed present in the X-ray spectrum, with ΔE ≲ 0.15 keV, this would mean that the inclination angle is ι ≲ π/4. Alternatively, if the source is indeed able to produce double Fe Kα lines with energy separation above ΔE ∼ 0.15 keV, the two black holes could have been observed in a state in which they are aligned and hence the radial component of the velocity could be negligible. However, this is highly unlikely since the source has been observed more than once by Swift-XRT, Suzaku and XMM-Newton at epochs that are not spaced by half periods, and in none of these observations has a possible double Fe Kα line been detected, which precludes the aligned black hole hypothesis.
Given that MCG+11-11-032 was reported as a possible binary SMBH by Severgnini et al. (2018), we also analyze the light curve of this Seyfert 2 galaxy, finding a best-fit period of P0 = 26.3 ± 0.6 months, with a goodness of fit of . By visual inspection, Severgnini et al. (2018) gave a rough estimate of the period of P0 ∼ 25 months, which is likely to be consistent with our result. From the SMBH mass of Lamperti et al. (2017), , derived from the velocity dispersion of the CO molecules, we infer that the separation of the two black holes is pc, from which we can quickly compute . We expect an energy shift of , assuming an inclination angle , typically adopted for Seyfert 2 sources, and assuming that the orbital plane of the black holes is aligned with the AGN inclination. This result is highly consistent with the observed centroid energies of the two Fe Kα lines, found in Severgnini et al. (2018) at E1 = 6.16 ± 0.08 and E2 = 6.56 ± 0.15 keV, i.e., ΔE = 0.4 ± 0.2 keV. This strongly supports the hypothesis that the observed double-peaked Fe line and periodicity are both produced by the same physical effect, likely to be the presence of two SMBHs in close orbit around each other. Hence, it is reasonable to consider our result (based on the Swift-BAT light curve) and the Severgnini et al. (2018) result (based mostly on the double Fe K line in Swift-XRT data) as the results of two independent experiments of the same physical scenario; this allows us to combine the two p-values (see Section 5) and reject the null hypothesis at the combined confidence level of 2.9σ. The results for Mrk 915 and MCG+11-11-032 are summarized in Table 1.
Table 1. Main Properties of the Two Sources Analyzed in This Paper
| Source Name | Type | Identified as Candidate | Period (months) | χ2 p-value | dL (Mpc) | a (10−3 pc) | |
|---|---|---|---|---|---|---|---|
| Mrk 915 | Seyfert 1.5 | This paper | 35 ± 2 | 2.3 × 10−4 | 105 | 5 ± 1 | 0.034 ± 0.007 |
| MCG+11-11-032 | Seyfert 2 | Severgnini et al. (2018) | 26.3 ± 0.6 | 9.7 × 10−3 | 160 | 6.5 ± 1.5 | 0.06 ± 0.02 |
Note. We report the name of the source, the AGN type, the reference where it was first reported as a candidate SMBHB, the period obtained with a sinusoidal fit in units of months, the epoch folding p-value obtained with a χ2 test of the null hypothesis, the luminosity distance of the AGN, the separation between the two black holes under the assumption that the observed periodicity is due to a binary system, and their relative velocity.
Download table as: ASCIITypeset image
We note that the observed periodicity, in principle, may be produced by the circumbinary disk periodic accretion flow into the cavity, or by the modulated emission by the minidisks, which has the same period as the binary. However, as argued by Tang et al. (2018), the circumbinary emission is dominant in soft X-rays (E < 4–5 keV), while in hard X-rays, including the BAT energy band, the observed emission is dominated by the minidisk emission. Moreover, concerning MCG+11-11-032, the consistency between the observed energy shift between the two Fe Kα emission lines and the expected one inferred from the periodicity strongly favors the minidisk scenario. This means that the observed periodicity is likely to be the same as that of the binary system.
Both Mrk 915 and MCG+11-11-032 would likely emit continuous GWs with gravitational frequencies fgw = 2/P0 ≃ 22 nHz and fgw ≃ 30 nHz, respectively, close to the frequency where PTAs are most sensitive (e.g., Lentati et al. 2015; Moore et al. 2015; Shannon et al. 2015; Mingarelli et al. 2017; Arzoumanian et al. 2018). However, current PTA data sets are not sensitive enough for any of these two sources, since GW signals from a single source can currently be observed only for sources with at a distance of d ≲ 150 Mpc (Aggarwal et al. 2019). Therefore, the GWs emitted by both Mrk 915 and MCG+11-11-032 would be significantly below the current detection limit of PTAs.
While waiting for the first PTA detection and the improvement of the sensitivity curve, we find X-rays are a very promising tool for discovering possible SMBHBs. Longer light curves are required for two main reasons: (i) to confirm current candidates with a higher significance. Note that the current 105 month Swift-BAT data release samples only approximately three periods for Mrk 915 and only nearly four for MCG+11-11-032. For the latter, the 123 month data set has significantly improved detection, from 2.6σ to 3.4σ. The greater the number of data points we combine for each phase bin (see Section 4.2), the smaller the errors on the epoch folding, which results in a much better χ2 test. (ii) To find new candidates with the PSD selection criteria described in Section 4. In fact, by sampling longer continuous periods, while the noise level at a given frequency remains roughly constant, the periodic peak, if present, will be much higher at any additional sampled period. Longer Swift-BAT light curves, which will allow us to study the variability for up to ∼250 months, will therefore be crucial for periodicity studies. Additionally, the Wide Field Monitor on board the future Enhanced X-Ray Timing and Polarimetry Mission (Zhang et al. 2019) may continue the legacy of BAT even after the decommissioning of the Swift telescope.
It must be stressed that the present work does not represent a full statistical study of the SMBHB population in the local universe. First of all, it is limited to AGN, which are only ∼10% of the SMBHs in the observable universe, and there is no reason to privilege active over non-active galaxies. Second, the selection criteria include only the most prominent peaks and exclude sources with periodicities buried under a high level of noise. This is clear in the case of MCG+11-11-032, which is excluded from the PSD selection given its high level of non-periodic noise. This is also true for the method used in Liu et al. (2020), in which a cut in excess variance has been applied, because the PSD does not take photometric errors into account, leaving both Mrk 915 and MCG+11-11-032 out of their sample. However, we note that we obtain the same results in the coincident sample, even if the two methods are different. Moreover, concerning MCG+11-11-032, we stress that we are able to reject the null hypothesis above 3σ only when we consider the 123 month long light curve, which samples around five periods.
Finally, the detection of double-peaked Fe Kα lines is still in its pioneering stage. XMM-Newton, currently the instrument with the largest effective area in the Fe Kα spectral region, is only able to observe energy shifts ΔE ≳ 0.15 keV. Therefore, double Fe lines produced by orbital motions of SMBHBs with the range of periods analyzed in this work are only observable for a limited number of AGN, mostly those with edge-on inclinations. Future microcalorimeters such as the ones on board XRISM (e.g., XRISM Science Team 2020) and Athena (e.g., Barret et al. 2016) will revolutionize the search for binary SMBHs, being able to detect energy shifts down to ΔE ∼ 0.01 keV, and possibly opening the window for the search for double-peaked Fe Kα lines in many more Seyfert galaxies and quasars.
We thank the referee for useful comments that improved the quality of this paper. We thank Stefano Andreon, Alessandro Caccianiga, Sergio Campana, Sergio Frasca, Cristiano Palomba, Sara Rastello, Paolo Saracco and Fausto Vagnetti for discussions and suggestions. The authors acknowledge a financial contribution from agreements ASI-INAF n.2017-14-H.0 and n.I/037/12/0. C.C. acknowledges funding from the European Union's Horizon 2020 Research and Innovation Program under the Marie Sklodowska-Curie grant agreement No. 664931. A.S. is supported by the European Research Council through the CoG grant "B Massive," grant No. 818691. We acknowledge our use of public data from the Swift data archive.
Footnotes
- 16
Excess variance (e.g., Nandra et al. 1997) is a parameter that quantifies variability, defined as where S2 is the variance of the light curve and σ(x) is the photometric error.
- 17
It should be recalled that all real and simulated data are discrete, although to simplify the notations we will denote them as continuous throughout the whole article.
- 18
We remove four points associated with unusually short exposure times, and thus with anomalously large errors, during that specific month.


















































































![$a={\left[{{GMP}}_{0}^{2}/4{\pi }^{2}\right]}^{1/3}$](https://content.cld.iop.org/journals/0004-637X/902/1/10/revision1/apjabb3c3ieqn64.gif)






![$a={\left[{{GMP}}_{0}^{2}/4{\pi }^{2}\right]}^{1/3}=(6.5\pm 1.5)\times {10}^{-3}$](https://content.cld.iop.org/journals/0004-637X/902/1/10/revision1/apjabb3c3ieqn71.gif)





